Answer:
1.
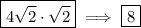
2.
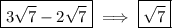
3.
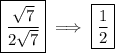
4.
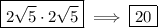
Explanation:
The Radical Rules by Lial et al. (2017) state that:
Product rule:
![\large \textsf{$\sqrt[n]{a}\cdot\sqrt[n]{b}=\sqrt[n]{ab}$}](https://img.qammunity.org/2023/formulas/mathematics/high-school/brobletqvtwhohlygzf3ya6v7mk58bo4xl.png)
- "The product of two roots is the root of the product."
Quotient rule:
![\large \textsf{$\sqrt[n]{(a)/(b)}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$}\ \ \textsf{$(b \\eq 0)$}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7h1irgaz0saba17tmvmlwgm1fwnzhb16hv.png)
- "The root of a quotient is the quotient of the roots."
1.
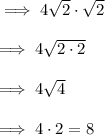
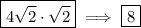
2.
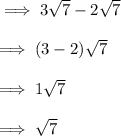
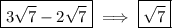
3.
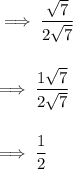

4.
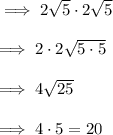
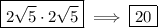
Reference:
Lial, M., Hornsby, J., Schneider, D., & Daniels, C. (2017). College Algebra and Trigonometry, Global Edition (6th ed., p. 94).