Answer:
(a) 12.5%
(b) 20%
(c) 96th
Explanation:
Let X denote the results of the 2018 SAT math exam.
It is provided that the mean of exam was, μ = 531 and standard deviation of σ 114.
Assume that X follows a normal distribution.
(a)
Compute the probability of test takers who scored lower than 400 on the math SAT as follows:
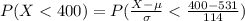
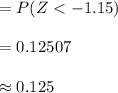
Thus, the percentage of test takers who scored lower than 400 on the math SAT is 12.5%.
(b)
Compute the probability of test takers who scored between 600 and 700 points as follows:
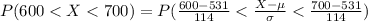

Thus, the percentage of test takers who scored between 600 and 700 points is 20%.
(c)
Compute the value of P (Z < 725) as follows:
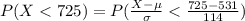
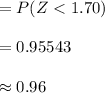
Thus, a student who scores 725 has a 96th percentile rank.