Question

Find the points at which the tangent line is horizontal for the given interval. F(x)=cosx-sinx [0,2pi]

Answer 1

`x=\{(3\pi)/(4), (7\pi)/(4)\}`

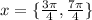
Explanation:

For the tangent line to be horizontal, the derivative of the function at that point must be 0.

Thus, let’s first take the derivative of our function:

`f ^\prime(x)=(d)/(dx)[\cos(x)-\sin(x)]`

Differentiate:

`f^\prime(x)=-\sin(x)-\cos(x)`

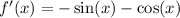
Now, let’s set our derivative equal to 0:

`0=-\sin(x)-\cos(x)`

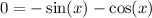
Let’s multiply everything by a negative:

`0=\sin(x)+\cos(x)`

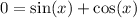
To solve for x, we can subtract sin(x) from both sides. This gives us:

`\cos(x)=-\sin(x)`

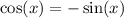
Now, we can refer to the unit circle. First, remember that the only points for which cosine is equal to sine is at the π/4 points. That is, π/4, 3π/4, 5π/4 or 7π/4.

However, cosine is equal to negative sine. The only two quadrants for which cosine and sine are the same but also have opposite signs is QII and QIV.

Therefore, our answers are 3π/4 and 7π/4.