Answer:
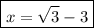
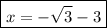
Explanation:
Solve for the value of
 :
:
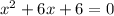
-When you use the quadratic formula (
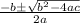 ), it would give you two solutions. So, use the quadratic formula:
), it would give you two solutions. So, use the quadratic formula:
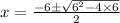
-Simplify
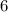 by the exponent
by the exponent
 :
:
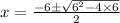
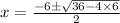
-Multiply both
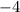 and
and
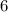 :
:
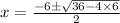

-Add
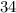 and
and
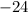 :
:


-Take the square root of
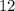 :
:


-Now solve the equation when
 is plus, So, add
is plus, So, add
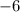 to
to
 :
:

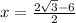
-Divide
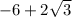 both sides by
both sides by
 :
:
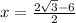
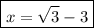 (Answer 1)
(Answer 1)
-Now solve the equation when
 is minus. So, Subtract
is minus. So, Subtract
 from
from
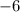 :
:
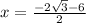
-Divide
 by
by
 :
:
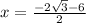
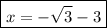 (Answer 2)
(Answer 2)