Question

Yumiko has a rectangular-shaped patio. She wants to double the area of the patio by increasing the length and the width by the same amount.

The length is 14 and the width is 10.

a. Write a function, in factored form, to calculate the number of feet Yumiko would need to add to the length and width.

b. What are the dimensions of the patio, rounded to the nearest hundredth feet?

I am not very good with completing the square and would like to understand it better. Any help would be very appreciated!

Answer 1

For a rectangle of length L and width W, the area is:

A = L*W

In this case, we start with:

L = 14ft

W = 10ft

Then the initial area is:

A = 14ft*10ft = 140ft^2

a) Now she wants to increase the same amount in each measure, then the new measures will be:

L = 14ft + x

W = 10ft + x

Now we want this new area to be twice the one that we got before, then the equation will be:

(14ft + x)*(10ft + x) = 2*140ft^2 = 280ft^2.

b) Let's solve the equation:

(14ft + x)*(10ft + x) = 280ft^2

First lets distribute the multiplication:

140ft + x*10ft + 14ft*x + x^2 = 280ft

Now let's group terms with the same power of x.

x^2 + (10ft + 14ft)*x + 140ft - 280ft = 0.

x^2 + 24ft*x - 140ft = 0.

Now we need to solve this quadratic equation, here we must use the Bhaskara equation for quadratic equations, and we will get two solutions for x.

`x = (-24ft +- √((24ft)^2 - 4*140ft*1) )/(2*1) = (-24ft +- 33.7ft)/(2)`

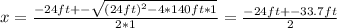
Then the two solutions are:

x = (-24ft - 33.7ft)/2 = -28.9 ft

This solution is negative, so it does not make sense and we can discard it.

x = (-24ft + 33.7ft)/2 = 4.85ft

This is positive, so we can use this.

Now we can find the new length and width:

L = 14ft + 4.85ft = 18.85ft

W = 10ft + 4.85ft = 14.85ft