Answer:
22
Explanation:
First, find the equation of the line in slope-intercept form, y = mx + b.
Using the coordinates of these two pairs, (48, -30) and (61, -45), the slope (m) can be calculated as follows:

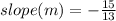
Find the y-intercept (b) by substituting x = 48, y = -30, and
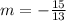 into y = mx + b:
into y = mx + b:
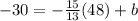
Solve for b.
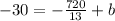
Add
 to both sides
to both sides

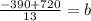
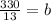
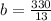
Substitute
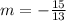 and
and
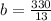 into y = mx + b
into y = mx + b
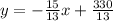
The x-intercept of the line with the above equation, would be the value of x when y = 0. This is the value of x where the line cuts across the x-axis. To calculate this, substitute y = 0 into
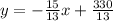 .
.
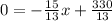
Subtract
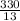 from both sides
from both sides
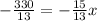
Divide both sides by
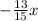
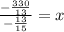

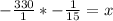
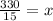
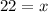
The x-intercept = 22