We want to see which position has the largest probability of winning the prize. We will find that the 18th person has the largest probability of winning.
We know that a person only will win the prize if that person has the same birthday that some in front of him/her.
So, the probability that the n-th person wins the prize is given by:
(probability that none of the persons in front share a birthday)*(probability of sharing a birthday with some of the n - 1 people in front).
Let's find the first one.
The first person can have a birthday in any of the 365 days.
The second person must not have the same birthday, so there are 364 options remaining.
The probability of this is just
p₂ = 364/365
For the third person, we have the same thing, this time, 363 remaining options:
p₃ = 363/365
For the (n - 1) person the probability is:
pₙ₋₁ = (365 - n + 2)/365
And the n-th person must share a birthday with some of the n persons in front of him, so there are (n - 1) options to choose, so the probability is:
pₙ = (n - 1)/365
Then, the joint probability is:
P = p₂*p₃*...*pₙ
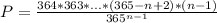
Now we have the equation, we just need to solve it for n such that we maximize the value of P in the range n ∈ [1, 50]
This is actually a really hard thing to find, but what you can notice, is that each time that n increases by 1, the denominator increases 365 times.
While the numerator increases by a factor:
(365 - n - 1)*n/(n - 1)
So we need to find the value of n such that the thing above is equal or smaller than 365.
Let's solve:
(365 - n - 1)*n/(n - 1) = 365
(365 - n - 1)*n = 365*n - 365
364*n - n^2 - 365*n + 365 = 0
-n^2 - n + 365 = 0
This is just a quadratic equation, the solutions are:
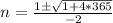
We only care for the positive solution, so we take:
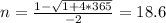
So, for the 19th person, the probability of winning will be smaller than for the 18th person, this happens because the numerator increased by a smaller factor than the denominator.
This means that the 18 person has the largest probability of winning.
If you want to learn more, you can read: