Question

ASSISTANCE PLEASE

The path of a projectile
launched from a 16-ft-tall tower
is modeled by the equation
y = −16x2 + 64x + 16. Graph the
equation. What is the maximum
height, in feet, reached by the
projectile?

(On a graph)

Answer 1

The maximum height reached by the projectile is 80 feet

Explanation:

Answer 2

The maximum height reached by the projectile is 80 feet

Explanation:

The given equation of the path of the projectile is y = -16·x² + 64·x + 16

Where;

y = The height in feet, reached by the projectile (Assumption)

x = The time it takes the projectile to reach the height, y (Assumption)

The shape of the given equation of the path of the parabola is that of a parabola turned upside down.

We have that the maximum height is given by the top of the curve where the curve changes direction, and the slope = 0

Therefore, we have;

`Slope = \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{\mathrm{d} \left (-16\cdot x^2 + 64\cdot x + 16 \right )}{\mathrm{d} x} = -32 \cdot x + 64 = 0`

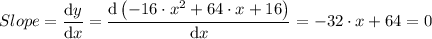
Therefore, at the maximum point, the slope is -32·x + 64 = 0

∴ x = -64/(-32) = 2 at the maximum point

The height at the maximum point = The maximum height,
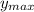`y_(max)`, is found by finding the value of y (the height) at x = 2 (the value of x at the maximum point)

Therefore, we have;

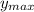`y_(max)` = -16 × 2² + 64 × 2 + 16 = 80 feet

The maximum height reached by the projectile,
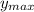`y_(max)` = 80 feet.