Answer: ±4 y ±6
Explanation:
Algunas definiciones:
Sea N un numero real.
El cuadrado de un numero es:
N^2.
Ahora, nos dicen que N es par, entonces podemos escribir:
N = 2*n
donde n es un numero entero.
Y el par consecutivo a N, va a ser M = N + 2.
M = 2*n + 2.
Entonces:
"La suma de los cuadrados de dos números reales pares consecutivos es 52"
(2n)^2 + (2n + 2)^2 = 52
Tenemos que resolver esto para n.
4n^2 + 4n^2 + 8n + 4 = 52
Entonces tenemos una ecuación cuadrática:
8*n^2 + 8n + 4 - 52 = 0
8*n^2 + 8n - 48 = 0
Antes de usar la ecuación de Bhaskara, dividamos todos los coeficientes por un factor común, en este caso 8 es un factor común:
(8*n^2 + 4n - 48)/8 = n^2 + n - 6 = 0.
Ahora resolvamos esto para n, las dos soluciones son
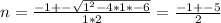
Entonces las dos soluciones son:
n = (-1 - 5)/2 = -3
n = (-1 + 5)/2 = 2
Entonces, si tomamos la primer solucion, los numeros consecutivos son:
N = 2*-3 = -6
M = N + 2 = -4
Si tomamos la segunda solucion, n = 2.
N = 2*2 = 4.
M = N + 2 = 6.
Entonces podemos concluir que las soluciones son:
±4 y ±6