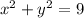Answer:
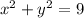
Explanation:
Equation of a circle
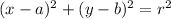
(where (a, b) is the center and r is the radius)
Given:
- center = (0, 0)
- point on circle = (-3, 0)
Substitute the given values into the formula and solve for r²:
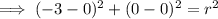
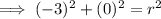
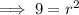
Substitute the center and found value of r² into the formula to determine the equation of the circle: