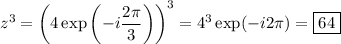Let z = -2 - 2√3 i.
Find the modulus of z :
|z| = √((-2)² + (-2√3)²) = √16 = 4
Find the argument of z (note that z lies in the third quadrant):
arg(z) = arctan(2√3/2) - π = arctan(√3) - π = -2π/3
Then in polar form, we have
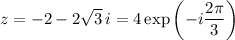
By DeMoivre's theorem, the cube of z is