Question

A bag weighing 80 N rests on a horizontal surface. The coefficient of static friction between the bag and the surface is 0.4, and the coefficient of kinetic friction is 0.2. What minimum horizontal force must be applied to keep the bag moving at constant velocity once it has started to move?

Answer 1

The minimum horizontal force that must be applied to keep the bag moving at constant velocity once it has started to move is 16 newtons.

Explanation:

According to the First and Second Newton's Laws, an object has net force of zero when it is at rest or moves at constant velocity. Given that bag rests on a horizontal surface, the equation of equilibrium is:

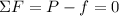`\Sigma F = P - f = 0` (Eq. 1)

Where:

`P` - Horizontal force exerted on the bag, measured in newtons.

`f` - Kinetic friction force, mesured in newtons.

From (Eq. 1), we get that horizontal force is:

`P = f`

On the case of a horizontal surface, normal force exerted from ground on the bag and kinetic friction force is:

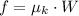`f = \mu_(k)\cdot W` (Eq. 2)

Where:

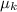`\mu_(k)` - Kinetic coefficient of friction, dimensionless.

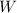`W` - Weight of the bag, measured in newtons.

Then we eliminate kinetic friction force by equalizing (Eqs. 1, 2):

`P = \mu_(k)\cdot W`

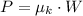
If we know that
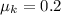`\mu_(k) = 0.2` and
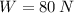`W = 80\,N`, then the horizontal force that must be applied to is:

`P =0.2\cdot (80\,N)`

`P = 16\,N`

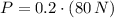
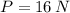
The minimum horizontal force that must be applied to keep the bag moving at constant velocity once it has started to move is 16 newtons.