Answer:
a) Two thorough rinses gives;
1/25 × 1/2 × 2/17 strong bleach/L = 1/425 strong bleach/L
b) The water should be divided into two quantities of 10 liters each
Explanation:
The given parameters are;
The initial volume of strong bleach solution in the nappies = 1/2 Liters
The volume of water first used to rinse = 12 liters
The volume of water used in the second rinse = 8 liters
Therefore, we have;
The total volume of the water and the concentrated bleach in the first rinse = 1/2 + 12 = 12.5 Liters
The new concentration of the bleach in the first rinse water = (1/2 strong bleach)/12.5 L = (1/2 strong bleach)/25/2 L = 1/2×2/25 = 1/25 strong bleach/L
The volume of the first rinse introduced in the second rinse = 1/2 Liters
The concentration of the bleach introduced in the second rinse = The new concentration of the bleach in the first rinse water = 1/25 strong bleach/L
The volume of water added in the second rinse = 8 liters
The total volume of the water and the bleach in the second rinse = (8 + 1/2) liters = 8.5 liters
The concentration of bleach in the second rinse = (The concentration of the bleach introduced in the second rinse × (Volume of bleach solution introduced in the second rinse))/(The total volume of the water and the bleach in the second rinse)
The concentration of bleach in the second rinse = (1/25 strong bleach/L × 1/2 L)/(8.5 Liters)
The concentration of bleach in the second rinse = (1/25 strong bleach/L × 1/2 L)/(17/2 Liters) = 1/25 × 1/2 × 2/17 strong bleach/L = 1/425 strong bleach/L
b) The the quantity of water in the first rinse = x
The amount of water in the second rinse = 20 - x
The concentration of bleach in the first rinse = 1/2/(x + 1/2) = 1/(2·x + 1)
The concentration introduced in the second rinse = 1/2 × 1/(2·x + 1) = 1/(4·x + 2)
The total volume of water and bleach introduced in the second rinse = (20 - x + 1/2) = 20.5 - x
The concentration of bleach in the second rinse = 1/(4·x + 2)/(20.5 - x)
The minimum value for the concentration can be found from taking the derivative of the function for the concentration and equation to zero as follows;
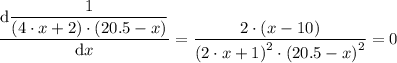
2·(x - 10) = 0
x = 0/2 + 10 = 10
x = 10
The the quantity of water in the first rinse = x = 10 liters
The the quantity of water in the first rinse = 10 liters
The amount of water in the second rinse = 20 - x = 20 - x = 20 - 10 = 10 liters
The amount of water in the second rinse = 10 liters
The water should be divided into two quantities of 10 liters each
Therefore, the water should be divided into two quantities of 10 liters each to give a final bleach solution concentration of 1/(4·x + 2)/(20.5 - x) = 1/(4×10 + 2)/(20.5 - 10) = 1/42 × 1/10.5 = 1/441 concentration/liter.