1 Answer

NeepNeepNeep · Answer 1 · 2023-02-21T15:10:19+0000

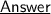
$\qquad\qquad\huge\underline{{\sf Answer}}$

Let's get it solved ~

We have been given length and width of a rectangle in terms of x ~

that is :

Area of the rectangle is given ~ i.e 24 unit²

Area of rectangle in terms of x is :

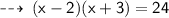
$\qquad \sf  \dashrightarrow \:(x - 2) \sdot(x + 3) = 24$

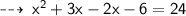
$\qquad \sf  \dashrightarrow \: {x}^(2) + 3x - 2x - 6= 24$

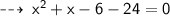
$\qquad \sf  \dashrightarrow \: {x}^(2) +x - 6 - 24 = 0$

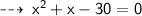
$\qquad \sf  \dashrightarrow \: {x}^(2) +x -30= 0$

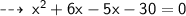
$\qquad \sf  \dashrightarrow \: {x}^(2) + 6x - 5x - 30 = 0$

$\qquad \sf  \dashrightarrow \: {x}^{}( x + 6) - 5(x + 6)= 0$

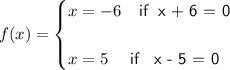
$f(x) = \begin{cases}x = - 6 \: \textsf{ \: if \:x + 6 = 0 } \\ \\ x = 5 \: \: \: \: \: \: \textsf{if \: x - 5 = 0} \end{cases}$

but since side of a rectangle can't be negative, we have to take value of x as 5

now, Perimeter of rectangle is ~

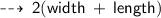
$\qquad \sf  \dashrightarrow \:2(width \: + \: length)$

$\qquad \sf  \dashrightarrow \:2(x - 2 + x + 3)$

$\qquad \sf  \dashrightarrow \:2(2x + 1)$

plug In the value of x ~

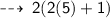
$\qquad \sf  \dashrightarrow \:2(2(5) + 1)$

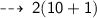
$\qquad \sf  \dashrightarrow \:2(10 + 1)$

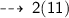
$\qquad \sf  \dashrightarrow \:2(11)$

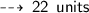
$\qquad \sf  \dashrightarrow \:22 \: \: units$

So, the correct choice is b~

Please log in or register to add a comment.