Question

Find the errors and solve the problem correctly!
Thanks

Answer 1

The sequence converges to 5 as n goes to ∞. We can prove this rigorously:

The claim is that, for
`n\in\Bbb N`,

`\displaystyle \lim_(n\to\infty) (5n-1)/(n+1) = 5`

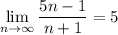
By definition of the limit, this means for any ε > 0, there exists some N such that for any n larger than N, we have

`\left| (5n-1)/(n+1) - 5 \right| < \varepsilon`

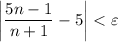
In order to ensure this inequality, we work backwards to find N in terms of ε :

`\left| (5n-1)/(n+1) - 5 \right| = \left| (5n-1 - 5(n+1))/(n+1) \right| = \frac4n+1 < \varepsilon`

n is a natural number, so n + 1 > 0 and |n + 1| = n + 1. Then

`\frac4{n+1} < \varepsilon \implies \frac{n+1}4 > \frac1\varepsilon \implies n+1 > \frac4\varepsilon \implies n > \frac4\varepsilon - 1`

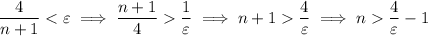
Let N be the smallest natural number greater than or equal to 4/ε - 1, i.e.

`N = \left\lceil \frac4\varepsilon - 1 \right\rceil`

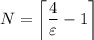
Then the proof follows: suppose

`n \ge N = \left\lceil \frac4\varepsilon - 1 \right\rceil`

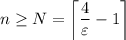
Then

`n \ge \left\lceil\frac4\varepsilon - 1\right\rceil \implies n > \frac4\varepsilon - 1 \\\\ \implies n+1 > \frac4\varepsilon \\\\ \implies \frac4{n+1} < \varepsilon \\\\\implies \left|(5n-1)/(n+1)-5\right| < \varepsilon`

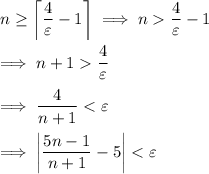
as required.

Or we can avoid the rigor and use some facts we know about limits:

`\displaystyle \lim_(n\to\infty) (5n-1)/(n+1) = \lim_(n\to\infty) (5-\frac1n)/(1+\frac1n) = 5`

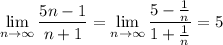
since 1/n converges to 0 as n goes to ∞.