Question

Write the balanced symbol equation for the electrolysis of aluminium oxide to produce aluminium, and the reduction of iron oxide with carbon to produce iron.

Then use that to calculate the atom economy for each.

Answer 1

Electrolysis of Al₂O₃: 4Al³⁺ (s) + 6O²⁺ (g) → 4Al (s) + 3O₂ (g)

Reduction of Elemental Fe: 2Fe₂O₃ (s) + 3C (s) → 4Fe (s) + 3CO₂ (g)

Atom Economy for Electrolysis of Al₂O₃: 52.9227%

Atom Economy for Reduction of Fe₂O₃: 62.8534%

Step-by-step explanation:

Step 1: Define Compounds

Aluminum Oxide - Al₂O₃

Iron Oxide - Fe₂O₃

Step 2: RxN

Al₂O₃ (s) → Al (s) + O₂ (g)

Fe₂O₃ (s) + C (s) → Fe (s) + CO₂ (g)

Step 3: Balance RxN

2Al₂O₃ (s) → 4Al (s) + 3O₂ (g)

• We need the same number of O on both sides (6 is the LCM)
• We will also need to balance the number of Al on both sides due to the change of O (4 reactant/product)

This is ONLY the decomposition reaction for Aluminum oxide, NOT the electrolysis.

2Fe₂O₃ (s) + 3C (s) → 4Fe (s) + 3CO₂ (g)

• We need the same number of O on both sides (6 is the LCM)
• We will also need to balance the number of Fe on both sides due to the change of O (4 reactant/product)
• We will also need to balance the number of C on both sides due to the change of O (3 reactant/product)

This is the final single-replacement reaction for the reduction of Iron Oxide to Iron.

Step 4: Electrolysis of Al₂O₃

We will have to use oxidation-reduction reactions (half-reactions). Let's break up the reaction into it's elements.

Al³⁺ + ? → Al

• To make the ion Al³⁺ turn into its neutral atom, we will need to add 3e⁻ to balance the half reaction

Al³⁺ + 3e⁻ → Al

O²⁻ → O₂ + ?

• Oxygen is a diatomic element, and in it's natural state is bonded to itself. We need to balance the half reaction

2O²⁻ → O₂ + ?

• We need to figure out how much electrons the ion O²⁻ loses to turn into its neutral atom. We see that we will need to lose 4e⁻

2O²⁻ → O₂ + 4e⁻

Our half reactions:

Al³⁺ + 3e⁻ → Al

2O²⁻ → O₂ + 4e⁻

• We now need balance the entire half reaction. Our LCM is 12

4 (Al³⁺ + 3e⁻ → Al) = 4Al³⁺ + 12e⁻ → 4Al

3 (2O²⁻ → O₂ + 4e⁻) = 6O²⁻ → 3O₂ + 12e⁻

• Add the 2 half reactions

4Al³⁺ + 12e⁻ + 6O²⁺ → 4Al + 3O₂ + 12e⁻

• Cancel out spectator ions/e⁻ to get our final half reaction

4Al³⁺ (s) + 6O²⁺ (g) → 4Al (s) + 3O₂ (g)

Step 5: Atom Economy

According to GCSE and my own deciphering, your equation for Atom Economy is essentially calculating for something similar to percent yield (but not quite).

`Atom \hspace{3} Economy \hspace{3} = \hspace{3} \frac{Molar \hspace{3} Mass \hspace{3} of \hspace{3} Product}{Molar \hspace{3} Mass \hspace{3} of \hspace{3} All \hspace{3} Reactants} \cdot 100 \%`

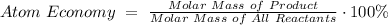
• 4Al³⁺ (s) + 6O²⁺ (g) → 4Al (s) + 3O₂ (g)

Molar Mass of Al - 26.98 g/mol

Molar Mass of O - 16.00 g/mol

Reactants: 4(26.98 g/mol) + 6(16.00 g/mol) = 203.92 g/mol

Products (Al as end product): 4(26.98 g/mol) = 107.92 g/mol

`Atom \hspace{3} Economy \hspace{3} = \hspace{3} \frac{107.92 \hspace{3} g/mol}{203.92 \hspace{3} g/mol} \cdot 100 \%=52.9227 \%`

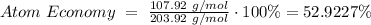
• 2Fe₂O₃ (s) + 3C (s) → 4Fe (s) + 3CO₂ (g)

Molar Mass of Fe - 55.85 g/mol

Molar Mass of O - 16.00 g/mol

Molar Mass of C - 12.01 g/mol

Reactants: 4(55.85 g/mol) + 6(16.00 g/mol) + 3(12.01 g/mol) = 355.43 g/mol

Products (Fe as end product): 4(55.85 g/mol) = 223.4 g/mol

`Atom \hspace{3} Economy \hspace{3} = \hspace{3} \frac{223.4 \hspace{3} g/mol}{355.43 \hspace{3} g/mol} \cdot 100 \%=62.8534\%`

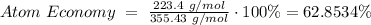
Step 6: Check for significant figures

Since we are not given any values, we don't really need to change any numbers to fit sig fig rules.