Answer:
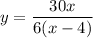
Explanation:
Keep in mind that a rational function with a vertical asymptote at
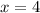 means the denominator must be 0 when
means the denominator must be 0 when
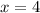 is plugged in.
is plugged in.
This means we have
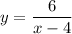 so far.
so far.
To account for the horizontal asymptote at
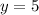 , we need to adjust the numerator and denominator so that they are the same degree and that the leading coefficients have a ratio of 5. We can do this by multiplying the numerator by 5x and the denominator by 6.
, we need to adjust the numerator and denominator so that they are the same degree and that the leading coefficients have a ratio of 5. We can do this by multiplying the numerator by 5x and the denominator by 6.
This leaves us with
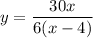 as the translated equation since the end behavior of the function is
as the translated equation since the end behavior of the function is
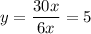 . See attached graph.
. See attached graph.