Answer:
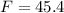
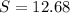
Explanation:
Given
Represent the sons age with S and the father's age with F
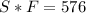

Required
Determine F and S
Substitute 5S - 18 for F in the first equation
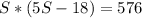
Open Bracket

Equate to 0

Solve using quadratic formula:
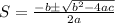
Where
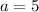
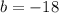

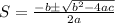

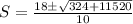
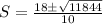
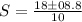
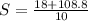 or
or
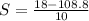
 or
or
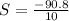
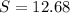 or
or
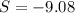
Since, age can't be negative.
We have that:
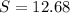
Recall that:

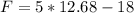
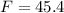
Hence:
The father is 45 years old and the son is 13 years old (Approximated)