Answer:
The reasonable number of days to reach Indianapolis is 3 days.
Explanation:
Total distance to be covered from Houston to Indianapolis, d= 1022 miles.
As they plan to drive between 425 and 475 miles/day, so the range of the rate of driving per day, r, is 425<r<475.
Let t day is the reasonable number of days to complete the journey.
As time = (distance)/(speed), so

The given range of the rate is
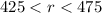
If
 , than
, than
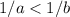 for
for
 ;
;
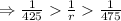
If a>b, the for any
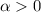 ,
,
 , so multiply the above equation by
, so multiply the above equation by
 , we have
, we have
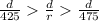
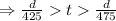 [from equation (i)]
[from equation (i)]
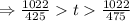 [given, d=1022 miles]
[given, d=1022 miles]
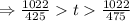

So, to cover the distance of 1022 miles, with the speed in between 425 miles/day and 475 miles/day, Jerry's family will take in between 2.40 days and 2.15 days. This means, for the given speed range, they need 2 complete days and some fraction of 3rd day to reach Indianapolis.
Hence, the reasonable number of days to reach Indianapolis is 3 days.