Question

The radius of the puddle is zero when time is zero but expands at a rate of one-quarter unit per second instead of one-half unit per second. By what factor does the denominator of the resultant composite function A(r(t)) change from that in the opening scenario?

Answer 1

Given that the radius of the puddle expands, originally, at a rate of 1/4 unit/second instead of 1/2 unit/second.

The current rate of expension of the radius,

\frac {r(t)}{t}=frac 1 4 unit/second ...(i)

The resultant composite function is area, A(r(t)).

The area of a circular region having radius r is,

`A(r)=\pi r^2`

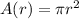
If the radius is the function of time, then the composite function is

`A(r(t))=\pi \(r(t))^2`

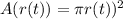
To determine the rate of change of area with respect to time, differentiate the composite function A(r(t)) once with respect to time, we have

`\frac {d\{A(r(t))\}}{dt}=\pi \left(2\frac {d\{r(t)\}}{dt}\right)`

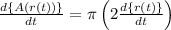
So, the composite function is changing twice of the rate of change of the radius.

By using equation (i), if r(i) is changing with R= 1/4 unit / second.

Then, A(r(t)) will change 2 x 1/4 = 1/2 square unit/second.