Answer:
Two possible locations on the coordinate plane for the park is B: (-1, 0) and D: (6, -1)
Step-by-step explanation:
Since we know the distance must be exactly 5 miles, that means the hypotenuse of the right triangle on the coordinate plane is equivalent to 5. Using this, we can solve which points are possible location points. For point A, the distances from the school would be 6 units left and 6 units down. The Pythagorean Theorem states that the sum of the two legs of a right triangle squared is equivalent to the hypotenuse squared. Since the leg lengths are 6 units, which is bigger than the hypotenuse, you know A is wrong. As for B, the distances from the school is 4 units left and 3 units down.
 +
+
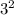 = 16 + 9 = 25, and
= 16 + 9 = 25, and
 = 25, so point B is a possible location on the coordinate plane for the park. Using this method, we can conclude point D is also a possible location, as the two distances are 3 right and 4 down, and you know
= 25, so point B is a possible location on the coordinate plane for the park. Using this method, we can conclude point D is also a possible location, as the two distances are 3 right and 4 down, and you know
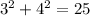 . So the correct answers are B and D
. So the correct answers are B and D