Answer:
1) 3.25 units
2) 4.875 seconds
3) 98.3125 units
4) 2.4375 seconds
Explanation:
1) The given equation of motion of the soft ball is y = -16·x² + 78·x + 3.25
Where;
y = The height of the softball
x = The time in seconds after it is hit
Therefore, the initial height of the softball is given by the value of y when x = 0 as follows;
y₀ = -16 × 0² + 78 × 0 + 3.25 = 3.25
Therefore, the initial height of the softball is 3.25 units
2) Given that the initial height of the soft ball is 3.25 ft., we have;
y = -16·x² + 78·x + 3.25 = x·(-16·x + 78) + 3.25
Therefore, the times at which the level of the softball is at 3.25 unit height, are;
x = 0 and ((-16·x + 78) = 0 which gives x = -78/(-16) = 4.875) 4.875 seconds
Therefore, from start time x = 0, the softball was in the air for 4.875 seconds
3) Given that the equation of motion of the softball is the equation of a parabola, the maximum height of the ball is given by the x-coordinate value at the top of the curve where the slope is zero as follows;
d(-16·x² + 78·x + 3.25)/dx = -32·x + 78 = 0
x = -78/(-32) = 39/16 = 2⁷/₁₆ = 2.4375 seconds
The maximum height of the softball is therefore;
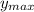= -16 × 2.4375² + 78 × 2.4375 + 3.25 = 98.3125
The maximum height of the softball is 98.3125 units
4) From the calculation for the maximum height, the time it took the softball to reach maximum height = 2.4375 seconds