Answer:
The maximum height above the ground the rocket reaches is 123.1 m.
Step-by-step explanation:
Let's find the final velocity at a distance of 200 m:
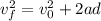
Where:
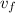 is the final speed =?
is the final speed =?
v₀ is the initial speed =0
a is the acceleration = 1.25 m/s²
d is the distance = 200 m
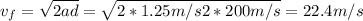
Now, when the engines of the rocket turn off and it is subject only to gravity, the height reached is:
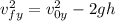
Where:
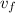 = 0
= 0
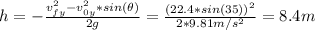
Finally, the maximum height above the ground is:

Where H is the vertical component of the 200.0 meters.
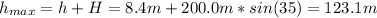
Therefore, the maximum height above the ground the rocket reaches is 123.1 m.
I hope it helps you!