Question

Water flows steadily through a 3.28-in-diameter pipe and discharges through a 1.64-in-diameter nozzle to atmospheric pressure. The flow rate is 26.5 gpm. (a) Calculate the minimum static pressure required in the pipe to produce this flow rate. (b) Evaluate the axial force of the nozzle assembly on the pipe flange.

Answer 1

A) 61.628 Ib/ft^2

B) 3.271 Ibf

Step-by-step explanation:

diameter of pipe = 3.28 inches

diameter of nozzle = 1.64 inches

flow rate = 26.5 gpm =

convert the flow rate to ft^3/s

= 26.5 gpm * 0.133681 ft^3/gallons * 1 min/ 60 seconds

= 0.059 ft^3/s

next we calculate the velocity in the pipe

Q =
`(\pi )/(4) d^(2) _(1) V1`

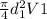
Q = 0.059

d1 = (3.28 / 12 )

hence V1 = ( 0.059 ) / (0.0747 * 0.7854 ) = 1 .01 ft/s

velocity in the Nozzle

Q =
`(\pi )/(4) d^(2) _(2) V2`

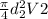
Q = 0.059

d2 = ( 1.64 /12 )

hence V2 = ( 0.059 ) / ( 0.7854 * 0.0187 ) = 4.02 ft/s

A) To determine the Minimum static pressure we apply the Bernoulli's equation

since the pipe and the Nozzle are at the same height the equation will be modified as

`(P1)/(w) + (V^2_(1) )/(2g) = (P2)/(w) + (v_(2) ^2)/(2g)`

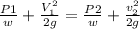
where w = 62.4 Ib/ft^3

V1 = 1.01

V2 = 4.02

P1 = ?

P2 = 0

g = 9.81

hence P1 ( static pressure ) = 62.4 * 0.772 = 61.628 Ib/ft^2

B) evaluate the axial force of the Nozzle assembly on the pipe flange

attached below is the detailed solution

Fx( axial force ) = -0.345 + 3.616 = 3.271 Ibf