Question

(a) Write down the Bernoulli's Equation and continuity Equation for a pipe flow and define each term in the equation. (b) The closed tank of a fire engine is partly filled with water, the air space above being under pressure. A 6 cm bore connected to the tank discharges on the roof of a building 2.5 m above the level of water in the tank. The friction losses are of 45 cm of water. Determine the air pressure which must be maintained in the tank to deliver 20 litres/sec on the roof.

Answer 1

A)
`(P)/(p) + (1)/(2) v^2 + gh = k\\`

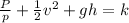
B ) 53.9 kN/m^2

Step-by-step explanation:

a) Bernoulli's equation and continuity equation for a pipe flow

`(P)/(p) + (1)/(2) v^2 + gh = k`

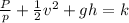
`(P)/(p)` = pressure head

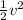`(1)/(2)v^2` = velocity head

gh = potential head

k = constant

p = density

b) determine the air pressure that must be maintained

Given data :

Discharge rate( R ) = 20 liters/sec ≈ 0.02 m^3

Bore diameter ( d ) = 0.06 m

first we calculate the velocity in the 6 cm bore

v =
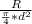`(R )/((\pi )/(4) *d^2)` ------- (2)

R = 0.02

d = 0.06

insert the given values into equation 2

V = 7.07 m/s

next we apply the Bernoulli's equation by rewriting it as follows

`(P)/(pg) + (1)/(2g) v^2 + h = k`

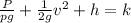
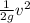`(1)/(2g)v^2` ( velocity head ) =
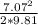`(7.07^2)/(2*9.81)` = 2.55

next we will apply the use of energy conservation law on the surface of water in tank and that on the roof :

Note : H1(frictional head loss ) = 45cm = 0.45 m , g = 9.81

applying the energy conservation law

`(P1)/(pg) + (1)/(2g) v_(1) ^2 + h1 =`
`(P2)/(pg) + (1)/(2g) v_(2) ^2 + h2`

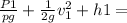
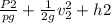
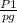`(P1)/(pg)` = 0 + 2.55 + 2.5 + 0.45

therefore ; P1 = 9.81 * 5.55 = 53.9 kN/m^2