Question

A major airline knows that about 2 percent of passengers do not manage to show up for their flight. Consider a small aircraft having 50 seats, and suppose that an airline sells precisely 50 tickets for a specific flight. Assuming that all passsengers are independent and have the same probability of not showing up, compute the probability that

Answer 1

a. The probability that the aircraft is fully occupied = 0.3642

b. The probability that between 1 and 5 (including 1 and 5) passengers do not show up is = 0.6354

Explanation:

From the given information:

We are to compute the probability that:

a. The aircraft is fully occupied( i.e. all the passengers show up)

b. Between 1 and 5 (including 1 and 5) passengers do not show up

Given that:

Percentage of passengers that do not show up = 2% = 0.02

And the population of the passengers = 50; since 50 tickets are being sold for a specific flight.

Let assume X be the random variable that follows a binomial distribution, thus, the number of passengers from the aircraft with 50 passengers can be represented as:

`X \sim Bin (n = 50, p =0.02)`

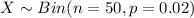
Thus;

The probability that the aircraft is fully occupied i.e. all the passengers show up is:

`= (1 - 0.02)^(50)`

= 0.98⁵⁰

= 0.3642

Hence, The probability that the aircraft is fully occupied = 0.3642

b. The probability that between 1 and 5 (including 1 and 5) passengers do not show up is:

= P(X = 1) + P(X =2) + P(X = 3) + P(X = 4) + P(X = 5)

=
`=(^(50)_1) 0.02(1-0.02)^(50-1) +(^(50)_2) 0.02(1-0.02)^(50-2) + (^(50)_3) 0.02(1-0.02)^(50-3) + ... + (^(50)_5) 0.02(1-0.02)^(50-5)`

`=(^(50)_1) 0.02(0.98)^(49) +(^(50)_2) 0.02(0.98)^(48) + (^(50)_3) 0.02(0.98)^(47) + ... + (^(50)_5) 0.02(0.98)^(45)`

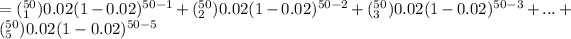
= 0.6354

Hence, The probability that between 1 and 5 (including 1 and 5) passengers do not show up is = 0.6354