Question

Calculate the pH of the buffer that results from mixing 60.0 mL of 0.25 M HCHO2(pKa= 3.74) and 15.0 mL of 0.500 M NaCHO

Answer 1

`pH=3.44`

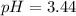
Step-by-step explanation:

Hello.

In this case, since the formic acid (HCHO2) is a weak acid and it is mixed with its conjugate base (CHO2⁻) in the form of NaCHO2, we can compute the pH via the Henderson-Hasselbach equation:

`pH=pKa+log(([Base])/([Acid]) )`

Whereas the concentration of both acid and base are computed considering final total volume of 75.0 mL after adding the volume of each solution as shown below:

`n_(base)=0.500mol/L*0.0150L=7.50x10^(-3)mol\\\\n_(acid)=0.25mol/L*0.0600L=1.5x10^(-2)mol`

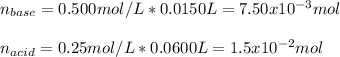
And the resulting concentrations upon the final volume:

`[Base]=(7.50x10^(-3)mol)/(0.0750L)=0.1M`

`[Acid]=(1.5x10^(-2)mol)/(0.0750L)=0.20M`

Thus, the pH is:

`pH=3.74+log((0.10M)/(0.20M) )\\\\pH=3.44`

Best regards.