Answer:
The 16 percent of the goldfish are smaller from 1.25 inches.
Explanation:
Let X denote the size of a particular goldfish.
It is provided that the mean size is, μ = 1.5 inches and standard deviation of the size is, σ = 0.25 inches.
Assume that X is normally distributed.
Compute the size of a goldfish such that only 16 percent of the goldfish are smaller from such size as follows:
P (X < x) = 0.16
⇒ P (Z < z) = 0.16
The z-value for such a probability is:
z = -0.99
*Use a z-table.
Compute the value of x as follows:
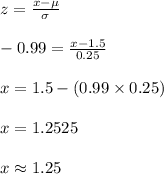
Thus, the 16 percent of the goldfish are smaller from 1.25 inches.