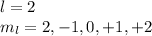Question

Protons can be accelerated to speeds near the speed of light in particle accelerators. Calculate the wavelength of a proton moving at 2.90 x 108 m/s if the proton was a mass of 1.673 x 10-24 g. 2. Give the values for the quantum numbers associated with the following orbitals a) 2p b) 3s c) 5d

Answer 1

(1) The wavelength of the proton is 1.366 x 10⁻¹⁵ m

(2) 2p( l = 1, ml = -1,0,+1)

3s( n = 3, l = 0, ml = 0)

5d ( l = 2, ml = -2,-1,0,+1,+2)

Step-by-step explanation:

Given;

mass of the proton; m = 1.673 x 10⁻²⁴ g = 1.673 x 10⁻²⁷ kg

velocity of the proton, v = 2.9 x 10⁸ m/s

The wavelength of the proton is calculated by applying De Broglie's equation;

`\lambda = (h)/(mv)`

where;

h is Planck's constant = 6.626 x 10⁻³⁴ J/s

Substitute the given values and solve for wavelength of the proton;

`\lambda = (h)/(mv)\\\\ \lambda = ((6.626*10^(-34)))/((1.673*10^(-27))(2.9*10^8))\\\\\lambda = 1.366 *10^(-15) \ m`

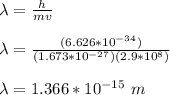
(2) the values for the quantum numbers associated with the following orbitals is given by;

n, which represents Principal Quantum number

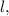`l,` which represents Azimuthal Quantum number

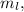`m_l,` which represents Magnetic Quantum number

(a) 2p (number of orbital = 3):

`l= 1\\m_l = -1,0,+1`

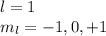
(b) 3s (number of orbital = 1):

`n= 3\\l=0\\m_l= 0`

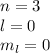
(c) 5d (number of orbital = 5)

`l=2\\m_l = 2, -1, 0, +1, +2`

Answer 2

1. λ = 1.4x10⁻¹⁵ m

2. a) n=2, l=1,
`m_(l)`= -1, 0, +1,
`m_(s)` = +/- (1/2)

b) n=3, l=0,
`m_(l)`= 0,
`m_(s)` = +/- (1/2)

c) n=5, l=2,
`m_(l)`= -2, -1, 0, +1, +2,
`m_(s)` = +/- (1/2)

Step-by-step explanation:

1. The proton's wavelength can be found using the Broglie equation:

`\lambda = (h)/(mv)`

Where:

h: is the Planck's constant = 6.62x10⁻³⁴ J.s

m: is the proton's mass = 1.673x10⁻²⁴ g = 1.673x10⁻²⁷ kg

v: is the speed of the proton = 2.90x10⁸ m/s

The wavelength is:

`\lambda = (h)/(mv) = (6.62 \cdot 10^(-34) J.s)/(1.673 \cdot 10 ^(-27) kg*2.90 \cdot 10^(8) m/s) = 1.4 \cdot 10^(-15) m`

2. a) 2p

We have:

n: principal quantum number = 2

l: angular momentum quantum number = 1 (since is "p")

`m_(l)`: magnetic quantum number = {-l,... 0 ... +l}

Since l = 1 →
`m_(l) = -1, 0, +1`

`m_(s)`: is the spin quantum number = +/- (1/2)

b) 3s:

n = 3

l = 0 (since is "s")

`m_(l)` = 0

`m_(s)` = +/- (1/2)

c) 5d:

n = 5

l = 2 (since is "d")

`m_(l)` = -2, -1, 0, +1, +2

`m_(s)` = +/- (1/2)

I hope it helps you!