Question

What value resistor will discharge a 2.60 μFμF capacitor to 20.0%% of its initial charge in 2.20 msms ? nothing Ω

Answer 1

The value of resistor is 525.76 ohms

Step-by-step explanation:

Given;

capacitance, C = 2.6 μF = 2.6 x 10⁻⁶ F

let the initial charge on the capacitor = Q₀

time , t = 2.2 ms = 2.2 x 10⁻³ s

The discharge of the capacitor is given by;

`Q(t) = Q_oe^{-(t)/(RC) }`

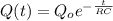
Where;

Q(t) is the charge after 2.2ms = 20% of Q₀ = 0.2Q₀

`Q(t) = Q_oe^{-(t)/(RC) }\\\\0.2Q_o = Q_oe^{-(t)/(RC) }\\\\0.2 = e^{-(t)/(RC) }\\\\ln(0.2) = -(t)/(RC)\\\\-1.6094 = -(t)/(RC)\\\\R = (t)/(1.6094C) \\\\R = (2.2*10^(-3))/(1.6094*2.6*10^(-6))\\\\R = 525.76 \ ohms`

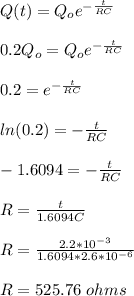
Therefore, the value of resistor is 525.76 ohms