Answer:
Fnet = 2782.6 N
Step-by-step explanation:
- Newton's 2nd Law states that the net force applied to an object, is equal to its mass times the acceleration.
- By definition, acceleration is the rate of change of velocity with respect to time, as follows:
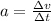
where Δv = vf - v₀ and Δt = tfi - t₀, replacing by the givens:
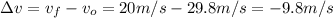
Δt = 4.9 s
⇒

- We can now apply Newton's 2nd Law, solving for Fnet, as follows:
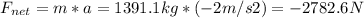
- The magnitude of the is net force (How large it is ) is just:
- Fnet = 2782.6 N