Answer:
When the ball is on the frictionless side of the track , the angular speed is 89.7 rad/s.
Step-by-step explanation:
Consider the ball is a solid sphere of radius 3.8 cm and mass 0.14 kg .
Given , mass, m=0.14 kg
Ball is released from rest at a height of, h= 0.83 m
Solid sphere of radius, R = 3.8 cm
=0.038 m
From the conservation of energy
ΔK = ΔU
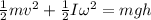
Here ,
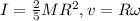
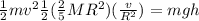
![(1)/(2) [v^2+(2)/(5)v^2]= gh](https://img.qammunity.org/2021/formulas/physics/college/vresh1dyheu8l9kj03xe3793ajnwfyf92h.png)
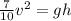

v=
![\sqrt{[gh/(0.7)]](https://img.qammunity.org/2021/formulas/physics/college/zahu9s0k5vvc4lihjat2dcvzd6xbozfmlk.png)
=
![\sqrt{ [(9.8 m/s^2)(0.83 m) / (0.7) ]](https://img.qammunity.org/2021/formulas/physics/college/3i4tdq95vc3uxyr9s21par29ervch4bx5z.png)
= 3.408 m/s
Hence, angular speed when it is on the frictionless side of the track,
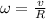
= (3.408 m/s)/(0.038 m)
 = 89.7 rad/s
= 89.7 rad/s
Hence , the angular speed is 89.7 rad/s