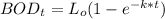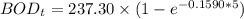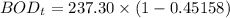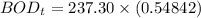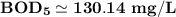Question

Some wastewater has a BOD5 of 150 mg/L at 20° C. The reaction rate k at that temperature has been determined to be 0.20/day. Find BOD5 (in mg/L) at 15° C.

Answer 1

The value of
`\mathbf{BOD_5 \ at \ 15^0 \ C \ is \simeq 130.14 \ mg/L}`

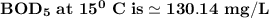
Step-by-step explanation:

From the given information:

To find the BOD5 (in mg/L) at 15° C; we need to know the ultimate carbonaceous BOD and the reaction rate coefficient at 15° C.

So, to start with the calculation of the ultimate carbonaceous BOD by using the formula:

`BOD_t = L_o (1-e^(-k*t))`

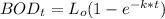
where;

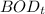`BOD _t` = Biochemical oxygen demand at t days

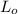`L_o` = the ultimate carbonaceous

∴

`150= L_o (1-e^(-0.20*5))`

`L_o =(150)/( (1-e^(-0.20*5)))`

`L_o =(150)/( (1-0.3679))`

`L_o =237.30 \ mg/L`

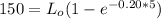
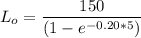
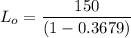
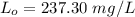
Thus, the ultimate carbonaceous BOD = 237.30 mg/L

For the reaction rate coefficient; we use the formula:

`k_(\tau) = k_(20) * \theta^(\tau - 20)`

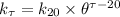
where;

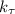`k_(\tau)` = rate of the reaction constant at various temperature (T) = 15

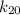`k_(20)` = rate of the reaction constant at standard laboratory = 0.20

`\theta` = constant = 1.047

∴

`k_(15) =0.20 * \theta^(15 - 20)`

`k_(15) =0.20 * 1.047^(-5)`

`k_(15) =0.20 *0.7948`

`k_(15) = 0.1590 / day`

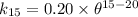
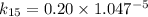
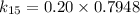
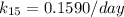
Thus, at 15° C, the reaction constant (k) = 0.1590 / day

Finally, the BOD5 (in mg/L) at 15° C can be calculated by using the formula:

`BOD_t = L_o (1 - e^(-k*t))`

`BOD_t = 237.30 * (1 - e^(-0.1590*5))`

`BOD_t = 237.30 * (1 -0.45158)`

`BOD_t = 237.30 * (0.54842)`

`\mathbf{BOD_5 \simeq 130.14 \ mg/L}`