Answer:
The volume V of the region = 80
Explanation:
The objective is to find the volume of the solid region bounded by z = 12 - y
Given that the portion of solid between the planes z = 12 - y and z = y; over the region R in the xy - plane bounded by y = x² and y = 6 - x²
Thus; R = { (x,y)/-2 ≤ x ≤ 2, x² ≤ y 6 - x² }
Then the volume is computed as follows:
![V = \int \int_R [(12 -y) -y] \ dy. dx](https://img.qammunity.org/2021/formulas/mathematics/college/lh81ypngsaf0s1yo1nxc7popcza2ebsk3l.png)
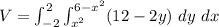
![V = \int^2_(-2)[ (12y-y^2]^(6-x^2)_(x^2) \ dx](https://img.qammunity.org/2021/formulas/mathematics/college/w3gnnk8ovra9nip4jsmgnadgkqj72c5ko5.png)
![V = \int^2_(-2) \begin {bmatrix}{ 12 [6-x^2-x^2] - [(6-x^2)^2-(x^2)^2] \end {bmatrix} \ dx](https://img.qammunity.org/2021/formulas/mathematics/college/6f4ph4aa0gcsvlhwv4y68tu75l92adk91m.png)
![V = \int^2_(-2) \begin {bmatrix}{ 12 [6-2x^2] - [36-12x^2]] \end {bmatrix} \ dx](https://img.qammunity.org/2021/formulas/mathematics/college/ziks0z0nbvlkeucnzayz6fc1huutvz5xdv.png)
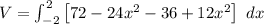
![V = \int^2_(-2) [36-12x ^2] \ dx](https://img.qammunity.org/2021/formulas/mathematics/college/b5tuihhcocxwkuahzopdvby75cnz91fate.png)
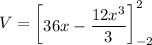

V = 80