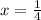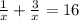
This is how to solve your problem:
- Combine fracrions with common denominator
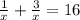
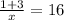
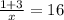

- Multiply all terms by the same value to eliminate fraction denominators

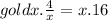
- Cancel multiplied terms that are denominator
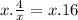

- Re-order terms so constants are on the left
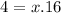
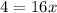
- Divide boths sides by the same factor
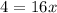
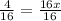
- divide the numbers
- Cancel terms that are in both the numerator and denominator
- Move the variable to the left
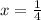
the final answer is :