Answer:
The probability that all three of them will find full-time jobs within three months after graduation from college is 0.0197.
Explanation:
Let X denote the number of college graduates who will find a full time job within three months after graduation from college.
A random sample of 3 college students, who will be graduating soon, are selected.
The probability of X is, p = 0.27.
Each student is independent of the other to find a full time job within three months after graduation from college.
The random variable X follows a binomial distribution with parameter n = 3 and p = 0.27.
Compute the probability that all three of them will find full-time jobs within three months after graduation from college as follows:
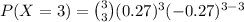
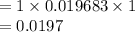
Thus, the probability that all three of them will find full-time jobs within three months after graduation from college is 0.0197.