Question

Consider the population of electric usage per month for houses. The standard deviation of this population is 128 kilowatt-hours. What is the smallest sample size to provide a 90% confidence interval for the population mean with a margin of error of 30 or less

Answer 1

Answer: 50

Explanation:

Formula for sample size(n) if population standard deviation
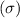`(\sigma)` is known:

`n=((\sigma* z_c)/(E))^2` , E = Margin of error ,
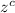`z^c` = Critical z-value

As per given,

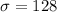`\sigma= 128` kilowatt-hours.

Critical z-value for 90% confidence = 1.645

E = 30

Required sample size :
`n=((128*1.645)/(30))^2=(7.01867)^2`

`=49.2617285689\approx50`

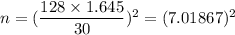
Hence, the smallest sample size to provide a 90% confidence interval for the population mean with a margin of error of 30 or less = 50