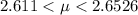Complete Question
Find the range for the population mean value with 95% and 65% confidence intervals for each set of data.
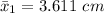 ,
,
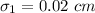 ,
,
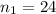 ,
,
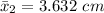 ,
,
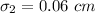 ,
,
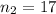
Answer:
The range for the population mean value with 95% confidence intervals for the first set of data is
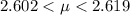
The range for the population mean value with 95% confidence intervals for the second set of data is
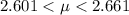
The range for the population mean value with 65% confidence intervals for the first set of data is
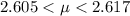
The range for the population mean value with 65% confidence intervals for the second set of data is
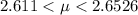
Explanation:
Generally the range for the population mean value with 95% confidence intervals for the first set of data is mathematically evaluated as follows
Generally the degree of freedom is mathematically evaluated as
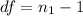
=>
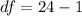
=>
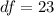
From the question we are told the confidence level is 95% , hence the level of significance is
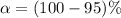
=>

Generally from the t distribution table the critical value of at is
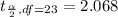
Generally the margin of error is mathematically represented as
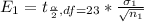
=>
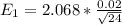
=>
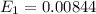
Generally 95% confidence interval is mathematically represented as
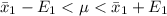

=>
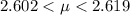
Generally the range for the population mean value with 95% confidence intervals for the second set of data is mathematically evaluated as follows
Generally the degree of freedom is mathematically evaluated as
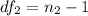
=>
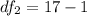
=>
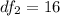
From the question we are told the confidence level is 95% , hence the level of significance is
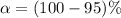
=>

Generally from the t distribution table the critical value of at is

Generally the margin of error is mathematically represented as
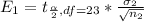
=>
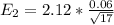
=>
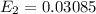
Generally 95% confidence interval is mathematically represented as
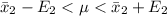
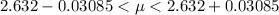
=>
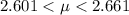
Generally the range for the population mean value with 65% confidence intervals for the first set of data is mathematically evaluated as follows
Generally the degree of freedom is mathematically evaluated as
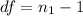
=>
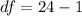
=>
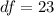
From the question we are told the confidence level is 95% , hence the level of significance is
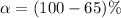
=>
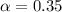
Generally from the t distribution table the critical value of at is
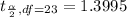
Generally the margin of error is mathematically represented as
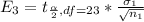
=>
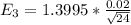
=>
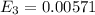
Generally 95% confidence interval is mathematically represented as
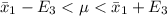
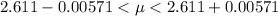
=>
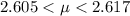
Generally the range for the population mean value with 65% confidence intervals for the second set of data is mathematically evaluated as follows
Generally the degree of freedom is mathematically evaluated as
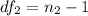
=>
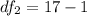
=>
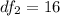
From the question we are told the confidence level is 95% , hence the level of significance is
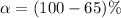
=>
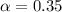
Generally from the t distribution table the critical value of at is
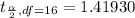
Generally the margin of error is mathematically represented as
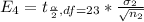
=>
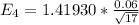
=>
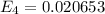
Generally 95% confidence interval is mathematically represented as
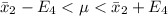
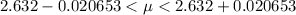
=>