Answer: 0.375
Explanation:
Given: The difference between actual and predicted weekly sales of a company follows a uniform distribution between -$4000 and $4000.
Probability density function:
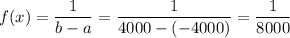
The probability that the actual sale is within $1500 of the predicted sale =
![\int^(1500)_(-1500)f(x)dx=\int^(1500)_(-1500)(1)/(8000)dx=(1)/(8000)[x]^(1500)_(-1500)\\\\= (1)/(8000)(1500-(-1500))\\\\= (1)/(8000)(3000)=0.375](https://img.qammunity.org/2021/formulas/mathematics/college/z2w19buh27z5r9ol1b6hmdm3gj0sm7dncc.png)
Hence, Required probability =0.375