Question

The scores for math test #3 were normally distributed. If 15 students had a mean score of 74.8% and a standard deviation of 7.57, how many students scored above an 85%?

Answer 1

Answer: 1 student scored above an 85%.

Explanation:

Let X = percentage score in test (normally distributed).

Given: Sample size = 15 , mean score :
`\mu`= 74.8% = 0.748 ,standard deviation :
`\sigma=7.57`

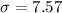
Now, The probability that student scores above 85%:

`P(X>85)=P((X-\mu)/(\sigma)>(85-74.8)/(7.57))\\\\=P(Z>1.347)\\\\=1-P(Z<1.347)\\\\=1-0.9110= 0.089`

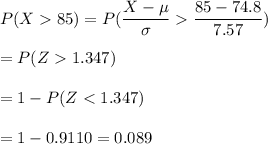
Probability that student scores above 85% = 0.089

Number of students scored above an 85% = 0.089 x 15 = 1.335 ≈ 1

hence, 1 student scored above an 85%.