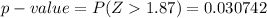Question

Consider versus A random sample of 35 observations taken from this population produced a sample mean of 40.27. The population is normally distributed with Calculate the p-value. Round your answer to four decimal places.

Answer 1

Complete Question

Consider H0: μ=38 versus H1: μ>38. A random sample of 35 observations taken from this population produced a sample mean of 40.27. The population is normally distributed with σ=7.2.

Calculate the p-value. Round your answer to four decimal places.

Answer:

The
`p-value = 0.030742`

Explanation:

From the question we are told that

The population mean is
`\mu = 38`

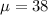
The sample size is n = 35

The sample mean is
`\= x = 40.27`

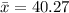
The standard deviation is
`\sigma = 7.2`

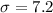
The null hypothesis is
`H_o`: μ=38

The alternative hypothesis is H1: μ>38

Generally the test statistics is mathematically represented as

`t = ( \= x -\mu )/((\sigma )/( √(n) ) )`

=>
`t = ( 40.27 - 38 )/(( 7.2 )/( √( 35) ) )`

=>
`t =1.87`

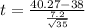
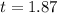
Generally from the z table the p-value of
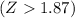`(Z > 1.87 )` is

`p-value = P(Z > 1.87) = 0.030742`