Answer:
Airplane covers a distance of approximately 50.265 feet in 4 minutes.
Explanation:
From Rotation Physics we know that angular speed is the number of revolutions done by a particle at a given time. If the boy is twirling a model airplane at constant speed, then we calculate such variable as follows:
 (Eq. 1)
(Eq. 1)
Where:
 - Angular speed, measured in revolutions per minute.
- Angular speed, measured in revolutions per minute.
 - Number of revolutions done by airplane, measured in revolutions.
- Number of revolutions done by airplane, measured in revolutions.
 - Time, measured in minutes.
- Time, measured in minutes.
Now we clear the number of revolutions done by airplane within expression:
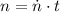
If we know that
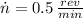 and
and
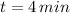 , then we get that number of revolutions is:
, then we get that number of revolutions is:
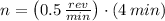
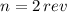
The airplane made two revolutions in four minutes.
Now, the distance covered by the airplane (
 ), measured in feet, is calculated by means of the equation below:
), measured in feet, is calculated by means of the equation below:
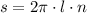
Where:
 - Length of the string, measured in meters.
- Length of the string, measured in meters.
 - Number of revolutions done by airplane, measured in revolutions (dimensionless).
- Number of revolutions done by airplane, measured in revolutions (dimensionless).
If we get that
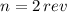 and
and
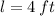 , then the distance covered by the airplane in 4 minutes is:
, then the distance covered by the airplane in 4 minutes is:
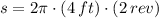
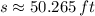
Airplane covers a distance of approximately 50.265 feet in 4 minutes.