Question

At its peak, a tornado is 73.0 m in diameter and carries 395-km/h winds. What is its angular velocity in revolutions per second

Answer 1

The angular velocity of the tornado at its peak is 0.478 revolutions per second.

Step-by-step explanation:

Let consider that tornado rotates at constant speed. From Rotation Physics we get the following relationship between linear (
`v`) and angular speeds (
`\omega`), measured in meter per second and radians per second, respectively.

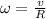`\omega = (v)/(R)` (Eq. 1)

Where
`R` is the radius of the tornado, measured in meters.

If we know that
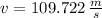`v = 109.722\,(m)/(s)` and
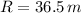`R = 36.5\,m`, then the angular speed of the tornado at its peak is:

`\omega = (109.722\,(m)/(s) )/(36.5\,m)`

`\omega = 3.006\,(rad)/(s)`
`\left(0.478\,(rev)/(s) \right)`

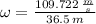
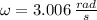
The angular velocity of the tornado at its peak is 0.478 revolutions per second.