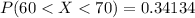Answer:
The value is
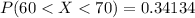
Explanation:
From the question we are told that
The mean is

The standard deviation is
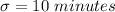
Generally the 1 hour is equivalent to 60 minutes
Generally the probability to complete the job in one hour or more, but less than 70 minutes is mathematically represented as

=>

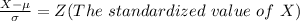
=>
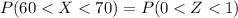
=>
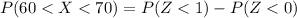
From the z table (Z < 1) and (Z < 0 ) is
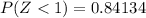
and
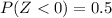
=>
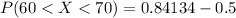
=>