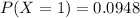Question

By some miracle, a Smudgy Press book is found to have 90% of its pages free of typographic errors. Assuming that the distribution of the typographical errors per page is Poisson, what is the probability that a randomly selected page contains exactly one error

Answer 1

The value is
`P(X = 1 ) = 0.0948`

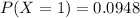
Explanation:

From the question we are told that

The the probability that the Smudgy Press book pages have zero errors
`p = 0.90`

Gnerally the probability distribution for Poisson distribution is

`P(X = x) = (\lambda ^x * e^(-\lambda))/(x!)`

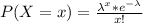
Gnerally the probability that the Smudgy Press book pages have zero errors is mathematically represented as

`P(X = 0) = (\lambda ^0 * e^(-\lambda))/(0!) =p= 0.90`

=>
`e^(-\lambda) =p= 0.90`

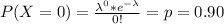
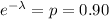
taking natural log of both sides

`ln (e^(-\lambda)) = ln(0.90)`

=>
`-\lambda = -0.1054`

=>
`\lambda = 0.1054`

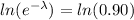
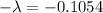
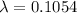
Generally the probability that a randomly selected page contains exactly one error is mathematically represented as

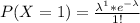
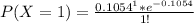
`P(X = 1 ) = (\lambda ^1 * e^(-\lambda))/(1!)`

=>
`P(X = 1 ) = (0.1054 ^1 * e^(-0.1054 ))/(1!)`

=>
`P(X = 1 ) = 0.0948`