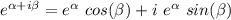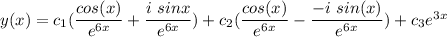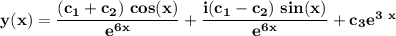Answer:
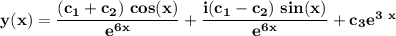
Explanation:
The objective of this question is to solve:
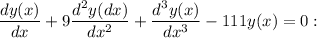
Suppose the general solution is proportional to
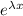 for
for
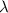 is constant; Then:
is constant; Then:
Let's replace
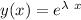 into the above equation:
into the above equation:
i.e.
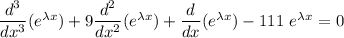
To Replace:
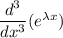 with
with
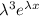
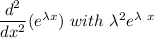
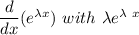
Thus;
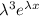 +
+
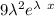 +
+
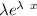 - 111
- 111
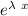 = 0
= 0
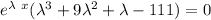
∴
In as much as
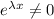 for any finite
for any finite
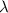 ; Then:
; Then:
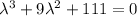
By Factorization:
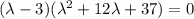
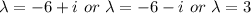
However;
The root
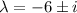 yield;
yield;
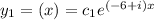
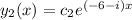
The root
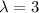 yield;
yield;
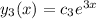
∴
The general solution is:
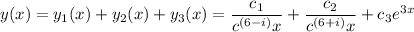
Using Euler's Identity ;