Question

At $0.31 per​ bushel, the daily supply for wheat is 306 ​bushels, and the daily demand is 459 bushels. When the price is raised to $0.79 per​ bushel, the daily supply increases to 546 ​bushels, and the daily demand decreases to 439 bushels. Assume that the​ price-supply and​ price-demand equations are linear. a. Find the​ price-supply equation.

Answer 1

The answer is below

Step-by-step explanation:

a) Find the price supply equation. b) Find the price demand equation. c) Find the equilibrium price and quantity.

Solution:

a) A linear equation is in the form y = mx + b, where m is the slope, y is a dependent variable, x is an independent variable, b is value of y at x = 0.

Let p represent the price and q represent the quantity. Hence we have the points (306, 0.31), (546, 0.79)

Using the formula:

`p-p_1=(p_2-p_1)/(q_2-q_1)(q-q_1)\\ \\p-0.31=(0.79-0.31)/(546-306) (q-306)\\\\p=0.002q-0.302`

b) Let p represent the price and q represent the demand. Hence we have the points (459, 0.31), (439, 0.79)

Using the formula:

`p-p_1=(p_2-p_1)/(q_2-q_1)(q-q_1)\\ \\p-0.31=(0.79-0.31)/(439-459) (q-459)\\\\p=-0.024q+11.326`

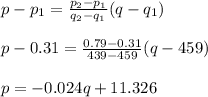
c) At equilibrium, price supply equation = price supply equation

0.002q - 0.302 = -0.024q + 11.326

0.002q + 0.024q = 11.326 + 0.302

0.026q = 11.628

q = 447.23 bushels

p = 0.002q - 0.302 = 0.002(447.23) - 0.302

p = $1.2