Question

The pH of a solution of 19.5 g of malonic acid in 0.250 L is 1.47.The pH of a 0.300 M Solution of sodium hydrogen malonate is 4.26. What are the values of Ka1and Ka2

Answer 1

`Ka_1=1.61x10^(-3)`

`Ka_2=1.01x10^(-8)`

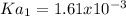
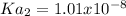
Step-by-step explanation:

Hello.

In this case, since the stepwise dissociation of malonic acid which is a diprotic acid that we are going to symbolize by H₂A, is:

`H_2A\rightleftharpoons H^++HA^-;Ka_1\\\\HA^-\rightleftharpoons H^++A^-;Ka_2`

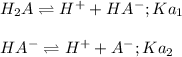
The first ionization has the following equilibrium expression:

`Ka_1=([H^+][HA^-])/([H_2A])`

Whereas the concentration of H⁺ equals the concentration of HA⁻ and is computed via the pH:

`[H^+]=[HA^-]=10^(-pH)=10^(-1.47)=0.0339M`

Next, we compute the molarity of the 19.5 g of malonic acid (molar mass = 104.06 g/mol) as shown below:

`[H_2A]=(19.5g/(104.06 g/mol))/(0.250L)=0.750M`

Thus, Ka1 turns out:

`Ka_1=((0.0339)(0.0339))/(0.750-0.0339)=1.61x10^(-3)`

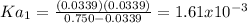
Now, for the second ionization, since the 0.300-M sodium hydrogen malonate is the source of HA⁻, and the pH is 4.26, we can compute the concentration of both H⁺ and A⁻² again by considering the pH:

`[H^+]=[A^-^2]=10^(-4.26)=5.50x10^(-5)M`

Therefore Ka2 turns out:

`Ka_2=([H^+][A^(-2)])/([HA^-])=((5.50x10^(-5))(5.50x10^(-5)))/(0.300-(5.50x10^(-5)))\\ \\Ka_2=1.01x10^(-8)`

Best regards!