Answer:
P(19)=$19,852
To the nearest dollar.
Explanation:
Exponential Growth
The natural growth of some magnitudes can be modeled by the equation:
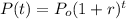
Where P is the actual amount of the magnitude, Po is its initial amount, r is the growth rate and t is the time.
We are given the condition that an investment of Po=$6,000 in an account doubles every 11 years. The final value of the investment in t=11 is P(11)=$12,000.
Substituting into the general equation:
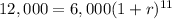
Dividing by 6,000 and swapping sides:
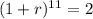
Taking the 11th root:
![1+r=\sqrt[11]{2}](https://img.qammunity.org/2021/formulas/mathematics/college/nl7t62c48qoavmzqwl6wreakmg1eqbmg6c.png)
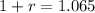
Substituting into the formula:
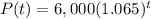
Now we need to find the money in the account after t=19 years:

P(19)=$19,852
To the nearest dollar.