Answer:
The 99% C.I is ( 367.703, 382.297 )
Explanation:
Given that:
sample mean
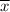 = 375
= 375
Population standard deviation
 = 20
= 20
Sample size n = 50
The level of significance
 = 1 - C.I = 1 - 0.99 = 0.01
= 1 - C.I = 1 - 0.99 = 0.01
From z tables:
The critical value =
 =
=
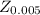 = 2.58
= 2.58
The margin of error E =


The margin of error E =
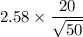
The margin of error E = 7.297
The limits of 99% C.I are expressed as:
Lower limit =
 = 375 - 7.297
= 375 - 7.297
Lower limit = 367.703
Upper limit =
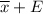 = 375 + 7.297
= 375 + 7.297
Upper limit = 382.297
The 99% C.I is
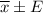 =
=
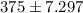
= ( 367.703, 382.297 )